Den allgemeinen Spannungszustand kann man durch sechs unabhängige Spannungen beschreiben. Diese sechs Spannungen bestehen aus 3 Normalspannungen und 3 Schubspannungen und werden im Spannungstensor dargestellt. Diese Spannungen beziehen sich auf ein willkürlich gewähltes Koordinatensystem (x,y,z). Das Koordinatensystem kann man beliebig drehen. Die Spannungen im Spannungstensor ändern sich dann, der Spannungszustand bleibt aber der gleiche. Es gibt also unendlich viele Möglichkeiten, ein und den selben Spannungszustand in einem Spannungstensor darzustellen.
Das Koordinatensystem kann so gedreht werden, dass nur noch Spannungen auf der Hauptdiagonale übrig bleiben. Das heißt, dass die Schubspannungen verschwinden und nur noch Normalspannungen übrig bleiben. Diese Normalspannungen werden Hauptspannungen genannt.
\(S=\begin{pmatrix}
\sigma_{1} & 0 & 0\\
0 & \sigma_{2} & 0\\
0 & 0 & \sigma_{3}
\end{pmatrix}\)
Um das Koordinatensystem so zu drehen wird mathematisch gesehen ein Eigenwertproblem gelöst (siehe auch Herleitung der Hauptspannungen für den ebenen Spannungszustand).
\(det \left( S – \sigma E \right)=0\)
S: Spannungstensor
E: Einheitsmatix
Für den ebenen Spannungszustand werden die Hauptspannungen nach der folgenden Formel berechnet:
\(\sigma_{1,2} = \frac{ 1}{ 2} \left( \sigma_x + \sigma_y \right) \pm \frac{ 1}{ 2} \sqrt{ \left( \sigma_x – \sigma_y \right)^2 + 4 \tau_{xy}^2 }\)
\(\sigma_x\), \(\sigma_y\): Spannungen in x- bzw. y-Richtung
\(\tau_{xy}\): Schubspannung
Die Richtung der Hauptspannungen wird nach der folgenden Formel berechnet:
\(tan \left( 2 \alpha \right) = \frac{\tau_{xy}}{\sigma_x – \sigma_y}\)
Glossar Festigkeitslehre
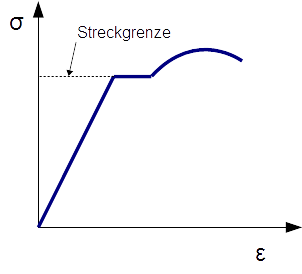
Die Streckgrenze ist die Spannung, bis zu der man einen linearen Zusammenhang zwischen Spannung und Dehnung annehmen kann. Bis zum Erreichen der Steckgrenze gilt das Hookesche Gesetz. Die Streckgrenze ist also die Grenze des elastischen Materialverhaltens. Wird die Belastung weiter erhöht, dann beginnt das Material zu fließen und das Material erhält eine bleibende plastische Verformung.
Für sie Streckgrenze sind verschiedene Formelzeichen im Gebrauch, z. B. \(R_e\) und \(\sigma_y\). Die Streckgrenze wird häufig in der Einheit N/mm² oder MPa angegeben.
Die Streckgrenze wird auch Fließgrenze oder Elastizitätslimit genannt.
Sie wird hauptsächlich für Stähle verwendet. Mit dem Zugversuch kann die Streckgrenze eines Materials ermittelt werden.
Bei Stahl lässt sich die Streckgrenze einfach bestimmen, da sie im Spannungs-Dehnungs-Diagramm eindeutig zu erkennen ist. Es gibt aber auch viele Materialien, bei denen die Streckgrenze nicht so ausgeprägt ist, z. B. bei Aluminium. Bei solchen Materialien wird häufig statt der Streckgrenze die 2 ‰-Dehngrenze verwendet.
Hier ein paar Werte für verschiedene Werkstoffe.
Baustahl nach EN 10025-2:2004-11
| Werkstoff |
Streckgrenze [N/mm²] |
| S 185 |
185 |
| S 235 |
235 |
| S 275 |
275 |
| S 355 |
355 |
| S 450 |
450 |
| E 295 |
295 |
| E 335 |
335 |
| E 360 |
360 |
Baustahl nach EN 10025-3:2004-11
| Werkstoff |
Streckgrenze [N/mm²] |
| S 275 N / NL |
275 |
| S 355 N / NL |
355 |
| S 420 N / NL |
420 |
| S 460 N / NL |
460 |
Baustahl nach EN 10025-4:2004-11
| Werkstoff |
Streckgrenze [N/mm²] |
| S 275 M / ML |
275 |
| S 355 M / ML |
355 |
| S 420 M / ML |
420 |
| S 460 M / ML |
460 |
Siehe auch:
Glossar Festigkeitslehre
Bei diesem Spannungszustand sind in einem Körper die drei Normalspannungen immer gleich groß, egal wie das Achsensystem gedreht wird. Außerdem treten keine Schubspannungen auf. Das bedeutet, dass die Normalspannungen auch immer Hauptspannungen sind. Jedes beliebige Achsensystem ist also ein Hauptachsensystem.
Der Spannungstensor für den hydrostatischen Spannungszustand sieht so aus:
\(S=\begin{pmatrix}
\sigma_{m} & 0 & 0\\
0 & \sigma_{m} & 0\\
0 & 0 & \sigma_{m}
\end{pmatrix}\)
\(\sigma_{m}\) ist die mittlere Normalspannung.
Siehe auch:
Quelle:
http://www.mech-albers.de/KontinuumAlbersDresden.pdf S. 66
Glossar Festigkeitslehre
Im Zusammenhang mit der Festigkeitslehre taucht immer wieder der Begriff „Spannungstensor“ oder „Spannungsmatrix“ auf. Erst einmal soll geklärt werden, was überhaupt eine Tensor ist.
Ein Tensor 0. Stufe ist nichts weiter als eine Zahl, genauer ein Skalar. Der Tensor 1. Stufe ist ein Vektor, ein Tensor 2. Stufe eine Matrix. Es gibt auch noch Tensoren höherer Stufe. Diese kann man sich so vorstellen:

Ein Beispiel für einen Tensor 4. Stufe ist der Elastizitätstensor.
Beim Spannungstensor handelt es sich um einen Tensor 2. Stufe, also eine Matrix.
Der Spannungstensor ist eine 3×3-Matrix und präsentiert den Spannungszustand eines Körpers an einer bestimmten Stelle.
\(
S=
\begin{bmatrix}
\sigma_{x} & \tau_{xy} & \tau_{xz}\\
\tau_{yx} & \sigma_{y} & \tau_{yz}\\
\tau_{zx} & \tau_{zy} & \sigma_{z}
\end{bmatrix}
\)
Diese Matrix enthält 6 unabhängige Größen.
- \(\sigma_{x}\)
- \(\sigma_{y}\)
- \(\sigma_{z}\)
- \(\tau_{xy}\)
- \(\tau_{xz}\)
- \(\tau_{yz}\)
Geschichtliches
Tensoren wurden zuerst in der Elastizitätstheorie verwendet. Die Verwendung des Spannungstensors geht auf Augustin-Louis Cauchy zurück.
Später verwendete James Clerk Maxwell Tensoren in der Elektrodynamik zur Beschreibung elektromagnetischer Felder.
Im Jahre 1905 erschien ein Aufsatz „Zur Elektrodynamik bewegter Körper“ in der Albert Einstein die Prinzipien von Maxwell auf die Bewegung von Körpern anwendete und damit die spezielle Relativitätstheorie begründetet.
Siehe auch:
Glossar Festigkeitslehre

