Beim ideal-elastisches Materialverhalten wird angenommen, dass das Hookesche Gesetz immer gilt. Dabei ist es egal, wie groß die Spannung wird. Spannung und Dehnung stehen immer in einem linearen Zusammenhang. Das Spannungs-Dehnungs-Diagramm sieht dann wie folgt aus:

Realistisch ist das nicht aber für die meisten Berechnungen ist diese Annahme völlig ausreichend. Treten Spannungen jenseits der Fließgrenze auf, dann kann über die Anwendung des ideal-plastischen Materialgesetzes nachgedacht werden. Die Frage ist allerdings, ob man wirklich die plastische Verformung zulassen möchte. Durch die wiederholte Plastifizierung kommt es zu einer Schädigung des Kristallgitters.
Glossar Festigkeitslehre
Führt man einen Zugversuch für ein Probestück aus Stahl durch, dann ergibt sich das folgende Spannungs-Dehnungs-Diagramm:
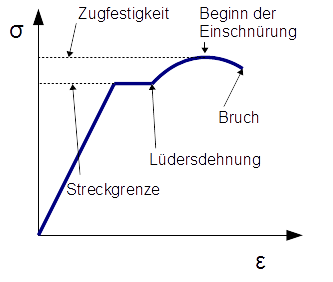
Will man die Plastifizierung in der Berechung mittels FEM-Software berücksichtigen, dann reicht es in den meisten Fällen aus, das nichtlineare Materialverhalten mit dem folgenden Diagramm näherungsweise abzubilden:
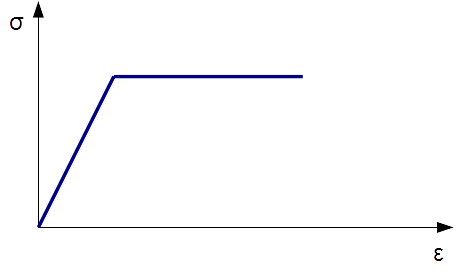
Mit diesem Diagramm wird im Rechenmodell ideal-plastisches Materialverhalten angesetzt. Der Verfestigungsbereich des realen Spannungs-Dehnungs-Diagramms wird vernachlässigt und es wird nur ein bilineares Materialgesetz verwendet.
Wenn die plastischen Verformungen klein sind, dann liefert das ideal-plastische Materialgesetz genaue Ergebnisse. Kleine Verformungen heißt, dass die Dehnungen unterhalb der Lüdersdehnung bleiben. Wird diese überschritten, dann liefert dieses Materialgesetz zu große Dehnungen, weil der Verfestigungsbereich des realen Spannungs-Dehnungs-Diagramms nicht berücksichtigt wird.
Glossar Festigkeitslehre
In der linearen Statik wird davon ausgegangen, dass das Hookesche Gesetz für beliebige Dehnungen gilt. Das entspricht aber nicht der Realität. Stahl beispielsweise beginnt beim Erreichen der Steckgrenze zu fließen. Solche Effekte werden materielle Nichtliniarität genannt.
Oft wird die materielle Nichtlinearität von Stahl durch ein bilineares Spannungs-Dehnungsdiagramm abgebildet.

Das ist eine Näherung. Das reale Materialverhalten ist komplizierter. Für die praktische Berechnung liefern solche Ansätze aber in der Regel ausreichend genaue Ergebnisse.
Es gibt aber noch viele andere Möglichkeiten der materiellen Nichtlinearität. Ein Werkstoff kann beim Erreichen einer bestimmten Spannung schlagartig versagen, also Reißen:

Das Verhalten für Druck und Zug kann unterschiedlich sein.

Beton ist beispielsweise ein Werkstoff, der Druckspannungen aufnehmen kann aber fast keine Zugspannungen.
Glossar Festigkeitslehre
Anisotropes Material hat Eigenschaften, die richtungsabhängig sind.
Eine besondere Form der Anisotropie ist die Orthotropie.
Glossar Festigkeitslehre
Im Gegensatz zu orthotropen Material ist bei isothropen Material die Steifigkeit in alle Richtungen gleich oder kann als gleich angenommen werden.
Die klassischen Vergleichsspannungshypothesen (Mises, Tresca, Rankine, Bach, Drucker-Prager, Mohr-Coulomb) sind für isotropes Material anwendbar.
Glossar Festigkeitslehre




